I am participating in InterviewStreet’s CodeSprint this weekend. It’s basically a 48-hour coding competition. Some of the problems are quite interesting, and I’ll be talking about them here. The first one I tried had this description:
You have an unbiased coin which you want to keep tossing until you get N consecutive heads. You’ve tossed the coin M times and surprisingly, all tosses resulted in heads. What is the expected number of additional tosses needed until you get N consecutive heads?
Input:
The first line contains the number of cases T. Each of the next T lines contains two numbers N and M.
Output:
Output T lines containing the answer for the corresponding test case. Print the answer rounded to exactly 2 decimal places.
Sample Input:
4
2 0
2 1
3 3
3 2
Sample Output:
6.00
4.00
0.00
8.00
The first step was to figure out how many tosses you need, on average, to get N consecutive heads. The probability of getting either a tail or a head is 1/2, so clearly you need 2 tosses on average to get one head. How about two?
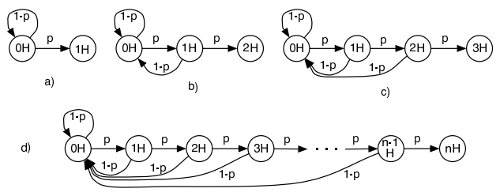
Obviously the result is not four tosses, because at each new coin tossed we need to consider the possibility of getting a tail, which erases any previous head that might have been tossed. The best way to illustrate this problem is with a Markov chain:
Figure a) represents the scenario where you want 1 head. You start from 0 heads, and from there you can either toss a tail or a head, where p is the probability of tossing a head. That diagram comes from an excellent paper I got on Cornell university (backup link).
Call A1 the number of tosses required to get 1 consecutive head. We can now say that:
A1 = (p)(1) + (1-p)(1+A1)
That is, A1 is equal to the probability of tossing a head right away, plus the probability of tossing a tail multiplied by 1+A1 (i.e., 1 wasted toss plus the A1 again, cause we still need to toss a head).
Re-organizing the equation you get that A1 = 1 / p, and since p in our case is 0.5 the result is 2, so 2 tosses on average are required to toss a head.
If you follow the maths in the paper you’ll realize that the number of tosses required to get N consecutive heads is 2^(n+1) – 2, so half our problem is solved.
Now we need to figure out the probability of getting N heads once you already have M heads tossed. I approached it with a recursive function:
#include <iostream>
#include <cstdio>
#include <cmath>
int tosses(int n){
int result = (int) pow(2,n+1) - 2;
return result;
}
float subTosses(int n, int m){
if (n==m)
return 1;
return 0.5 * (1+tosses(n)) + 0.5 * subTosses(n,m+1);
}
int main(){
int tests, m, n;
int i;
std::cin >> tests;
for (i=0;i<tests;i++){
std::cin >> n;
std::cin >> m;
if (n==m)
printf("0.00n");
else if (m==0)
printf("%.2fn",(float)tosses(n));
else{
printf("%.2fn",subTosses(n,m));
}
}
return 0;
}Apparently this is not the right answer, though, as my solution only got 1 out of 10 test cases right. Below you’ll find one of the solutions who passed all test cases:
#include<iostream>
#include<set>
#include<map>
#include<string>
#include<stdio.h>
#include<sstream>
#include<algorithm>
#include<queue>
#include<cmath>
#include<string.h>
using namespace std ;
void generate()
{
srand(time(NULL)) ;
char in[] = "in .txt" ;
for(int test = 0;test < 10;test++)
{
in[2] = test + '0' ;
FILE * fout = fopen(in,"w") ;
int runs = 100 ;
fprintf(fout,"%dn",runs) ;
for(int t = 0;t < runs;t++)
{
int n,m ;
if(test < 4) n = rand() % 50 + 1 ;
else n = rand() % 1000 + 1 ;
m = rand() % (n + 1) ;
fprintf(fout,"%d %dn",n,m) ;
}
}
}
int a[403] ;
void mul()
{
for(int i = 0;i < 400;i++) a[i] *= 2 ;
for(int i = 0;i < 400;i++)
{
a[i + 1] += a[i] / 10 ;
a[i] %= 10 ;
}
}
void add()
{
for(int i = 0;i < 400;i++)
{
if(a[i] < 9) { a[i]++ ; break ; }
else a[i] = 0 ;
}
}
void print()
{
int i ;
for(i = 399;i > 0;i--) if(a[i]) break ;
for(;i >= 0;i--) printf("%d",a[i]) ;
printf(".00n") ;
}
int main()
{
// generate() ; return 0 ;
int runs ;
cin >> runs ;
while(runs--)
{
int n,m ;
cin >> n >> m ;
n++ ; m++ ;
memset(a,0,sizeof a) ;
for(int i = 0;i < n;i++)
{
mul() ;
if(i < n - m) add() ;
}
print() ;
}
return 0 ;
}
Hey, you almost got it. Here’s my take on the problem:
When m == 0, the toss count is given by T(n, 0) = T(n-1, 0) + 1 + 0.5*T(n, 0). Solving for T(n, 0) and folding the recurrence results in T(n, 0) = 2^(n+1) – 2, as you point out above.
On the other hand, T(n, n) = 0, so we now have the base cases.
When n > m, T(n, m) = 1 + 0.5*T(n, m+1) + 0.5*T(n, 0) = 2^n + 0.5*T(n, m+1). Folding the redurrence results in T(n, m) = 2^(n+1) – 2^(m+1).
If you look at the solution provided, this is exactly what they are calculating (using an array of 400 decimal digits, as the results are huge!)
Hey, I cant understand how this T(n, m) = 2^(n+1) – 2^(m+1) happened.