Exponentiation is a very common part of mathematics, and it’s involved in many programming puzzles.

If you don’t have a function already implemented for you, a simple algorithm to compute a^b (a to the power of b) would be:
int expo(int a, int b){
int result = 1;
while (b>0){
result *= a;
b--;
}
return result;
}While this algorithm is relatively efficient, performing in liner time or O(n), it could be improved. In fact we could do the same task in O(log(n)+log(n)). How? By using a method called exponentiation by squaring.
Here’s the basic idea: for any a^b, if a b is even we could write it as (a^b/2)^2. If b is odd, on the other hand, we could write it as a * (a^(b-1/2))^2. Here’s a picture from Wikipedia which better illustrates it:
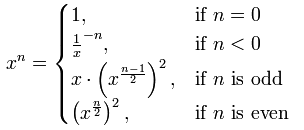
At each step we pretty much cut the problem in half, adding an extra multiplication for odd numbers. The recursive algorithm in C looks like this:
int expo(int a, int b){
if (b==1)
return a;
if (b==2)
return a*a;
if (b%2==0){
return expo(expo(a,b/2),2);
}
else{
return a*expo(expo(a,(b-1)/2),2);
}
}To test both algorithms I elevated every number from 1 up to 100,000,000 to the power of 30. Using the naive approach it took 7.1 seconds. Using the exponentiation by squaring one it took 3.9 seconds.
We can also treat the case where b is odd by re-writing it as a^b = a * a^(b-1), and break the treatment of even powers in two steps. This makes the algorithm easier to understand and a bit more efficient (surprisingly). The algorithm below took 3.4 seconds to complete the same task as above.
int expo(int a, int b){
int result;
if (b==2)
return a * a;
if (b==1)
return a;
if (b%2==1){
return a * expo(a,b-1);
}
else{
result = expo(a,b/2);
return result * result;
}
}And finally here’s the most optimized exponentiation by squaring algorithm I have seen around. It’s an iterative version where at each step you divide the exponent by two and square the base, and then for the iterations where the exponent is odd you multiply the result by the base. In theory at the odd iterations you would need to decrement the exponent by one, but this is not necessary because we’ll be performing integer division (i.e., 5/2 is equal to 4/2). The algorithm below took 2.2 seconds to complete the sake task as above:
int expo(int a, int b){
int result = 1;
while (b){
if (b%2==1){
result *= a;
}
b /= 2;
a *= a;
}
return result;
}We can squeeze a bit more of performance by using bitwise operations at the mod and divisor operators (it saves 0.15 seconds on the same task):
int expo(int a, int b){
int result = 1;
while (b){
if (b&1){
result *= a;
}
b >>=1 ;
a *= a;
}
return result;
}By the way, elevating all numbers from 1 to 100,000,000 to the power of 30 took 5.6 seconds with the standard library’s pow function. Sure, it uses double, but still it proves that if you are working with integers you might as well implement your own exponentiation function to make things more efficient.
There are some algorithms that are slightly more efficient, but they are much more complicated, so not worth the trouble in most cases. If you want to check them, though, visit the Wikipedia link above.
Thanks for posting! However, if you use the same code in Java, it only computes up to the 10th power I think.
Good One.nice.
Thanks!! It really helped a lot!! Great Algo!!
Nice! Thanks for sharing!
There is a typo on the last code (replacing /2 with shifting right):
if (b%2==1)
instead of
if (b%1)
thanks it worked! you are a god coder!
This is no typo. He wrote “b&1” which is equally to “b%2==1”, it is just a binary operator.
Think about the bits of an entry. If you compute “mod 2” you are only interested in the least significant bit. Therefore, a logical AND reveals, if the last bit is equal to 1 or 0 if you use “bitstring & 1”. If it returns 1, it is indeed the lsb set. That means this number has in its sum representation the 2^0 term set. Therefore: “bitstring mod 2 =1” in the same case.
This works with all powers of 2. Instead of “modulo 2^n” just use “& (2^n-1)”
Ok, had HW to implement fast exponentiation w/o recursion, used the second to last code. But I have a question:
I understand the algorithm. From a logical and mathematical point of view, it makes perfect sense. But I don’t understand the code.
Can someone explain this: We mention result 3x.
1. Initiation: int result = 1;
2. Returning: return result;
3. extra multiplication in case of odd exponent: result *= a;
Only in number 3 do we actively change result, so I can only fathom 2 results from this function: 1 and a (despite actually seeing this code work properly). So, how does result change in this code?
Boss can you explain me the fastest method of multiplying huge numbers (20to30digits long) in very very less time(for eg. Schonage Strassen algorithm). I read it on wikipedia but i didn’t understand various important concepts in it like fast fourier transform,discrete fourier transform,convolutions,etc. It was very very difficult for me to understand may be because i am too small to learn those concepts. I am searching for fastest multiplication method ever but i am unsuccessful. I love arithmetic very much so i am trying to learn these things though they are beyond my understanding but i have ability I want very very simple explanation .I will be very very very very helpful to you for any help that you may consider worthy. I hope you will surely help me.And thanks for such a beautiful explanation of exponentiation by squaring.
Very well! Thanks a lot!
Well this may work even faster :
int expo(int a, int b) //a-base b-power result-answer
{ long result;
result=a;
if(b==0)
{ return 1;
}
while(b>1)
{ if(b%2==0)
{ result=result*result;
}
else
result=result*result*a;
b/=2;
}
return result;
}
feroz, that won’t work.